- ผู้เขียน admin [email protected].
- Public 2023-12-17 03:45.
- แก้ไขล่าสุด 2025-06-01 06:49.
พื้นที่ที่ถูกแปลงและพื้นที่อยู่อาศัยเป็นพารามิเตอร์ที่สำคัญที่สุดสองประการที่ใช้ซ้ำ ๆ เพื่อกำหนดอาคารในสาขาวิชาที่หลากหลาย ในขณะที่สามารถกำหนดพื้นที่อยู่อาศัยได้ค่อนข้างง่าย แต่ลูกบาศก์มักจะทำให้เกิดปัญหาเสมอ สิ่งนี้รวมอะไรบ้างและสิ่งใดที่ถูกละเลยในการคำนวณ? เราอธิบายทีละขั้นตอนว่าคุณจะบรรลุผลที่เชื่อถือได้อย่างปลอดภัยได้อย่างไร
ลูกบาศก์คืออะไร?
คำว่า "ลูกบาศก์" มาจากภาษาละติน "ลูกบาศก์" และบรรยายถึงร่างกายโดยตรง อย่างไรก็ตาม ในกรณีของอาคาร เนื้อหานี้จะขยายคำจำกัดความและหมายถึงปริมาตรที่บ้านครอบครองโดยรวมโดยทั่วไปจะรวมผลรวมของไดรฟ์ข้อมูลต่างๆ ที่รวมกันเป็นไดรฟ์ข้อมูลทั้งหมด:
- ปริมาณสุทธิ: ปริมาณห้องที่ใช้งานได้ทั้งหมด “ปริมาณอากาศ” ในอาคาร
- ปริมาณการก่อสร้าง: ปริมาณส่วนประกอบทั้งหมดของอาคาร เช่น ผนัง เพดาน หลังคา ฯลฯ
ลูกบาศก์ยังคงมีอยู่ทั่วไปทุกหนทุกแห่งในภาษาทางเทคนิค แต่สำนวนที่ทันสมัยกว่านั้นคือ "พื้นที่ที่ถูกแปลง" สามารถพบได้ในกฎระเบียบปัจจุบัน ซึ่งโดยพื้นฐานแล้วจะอธิบายสิ่งเดียวกัน
ห้องแปลงมีวัตถุประสงค์อะไร?
คนธรรมดามักถามตัวเองอยู่เสมอว่าเหตุใดจึงต้องยุ่งยากกับการคำนวณลูกบาศก์ลูกบาศก์ การดูการใช้งานที่หลากหลายของค่านี้อย่างรวดเร็วทำให้ความหมายของค่านี้ชัดเจน:
- การวางแผนและติดตามต้นทุน
- ตัวบ่งชี้การประเมินกฎหมายการวางแผนอาคาร
- การเงินการก่อสร้าง
- ฐานในการกำหนดมูลค่ายุติธรรม
- แง่มุมส่วนบุคคล
หมายเหตุ:
คุณอ่านเกี่ยวกับสิ่งที่เรียกว่า "การสร้างมวลชน" ครั้งแล้วครั้งเล่าในวรรณกรรมเฉพาะทาง กฎหมายและข้อบังคับต่างๆ การกำหนดอาจแตกต่างกันไปบ้างขึ้นอยู่กับชุดของกฎ แต่สุดท้ายแล้วก็ยังเกี่ยวกับปริมาตรหรือพื้นที่ปิดด้วย
DIN277-1 เป็นพื้นฐานในการคำนวณ
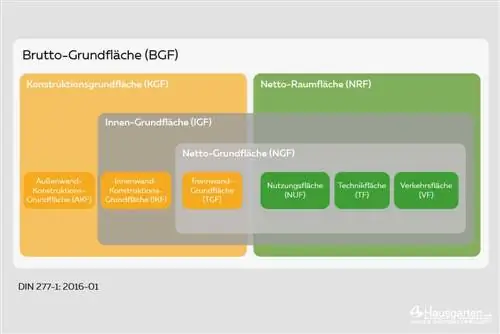
ตรงกันข้ามกับการกำหนดพื้นที่ใช้สอยหรือพื้นที่ใช้สอยซึ่งมีวิธีการกำหนดหลายวิธีเท่าๆ กัน พื้นฐานสำหรับการคำนวณลูกบาศก์เมตรมีความชัดเจนและเรียบง่าย ในเยอรมนี มีชุดกฎที่มีผลผูกพันซึ่งมีข้อกำหนดเฉพาะทั้งหมดสำหรับการกำหนดลูกบาศก์: DIN 277-1 “พื้นที่พื้นฐานและปริมาตรในการก่อสร้าง - ส่วนที่ 1: การก่อสร้างอาคาร”กฎระเบียบนี้ย้อนกลับไปถึงปี 1934 เมื่อมีการกำหนดปริมาตรอย่างสม่ำเสมอเป็นครั้งแรก ซึ่งต่อมาเรียกอย่างเป็นทางการว่าลูกบาศก์ หลังจากการเปลี่ยนแปลงและแก้ไขหลายครั้ง มาตรฐาน DIN เวอร์ชันปัจจุบันตั้งแต่ปี 2016 ก็เริ่มมีผลใช้บังคับในปัจจุบัน
ความสนใจ:
แม้ว่า DIN 277-1 จะไม่ใช่กฎหมาย แต่เป็นมาตรฐานที่ไม่สามารถใช้ได้โดยทั่วไป แต่ตอนนี้เป็นที่ยอมรับกันโดยทั่วไปและมีผลผูกพันอย่างแท้จริง ตามกฎทางเทคนิค ปัจจุบันเป็นส่วนหนึ่งของความทันสมัยที่ได้รับการยอมรับ และยังใช้เป็นข้อมูลอ้างอิงโดยศาลในกรณีที่มีข้อพิพาทอีกด้วย หากพื้นที่ปิดถูกคำนวณแตกต่างออกไป ก็เป็นไปได้ แต่ในกรณีที่มีข้อพิพาท จะต้องอาศัยความพยายามอย่างมากในการให้เหตุผลและพิสูจน์ความเท่าเทียมกัน
อะไรที่ต้องคำนึงถึงและสิ่งที่เหลืออยู่?
การดู DIN อย่างรวดเร็วจะทำให้เห็นได้อย่างชัดเจนว่าอะไรเป็นของลูกบาศก์และอะไรที่ไม่ใช่ ประโยคเกริ่นนำของมาตรา 7 “การกำหนดปริมาตรของอาคาร” ระบุเนื้อหาสำคัญอย่างชัดเจน:
“เนื้อหาปริมาตรรวม (BRI) รวมถึงปริมาตรของห้องทั้งหมดและโครงสร้างอาคารที่อยู่เหนือพื้นที่พื้นรวม (GFA) ของอาคาร”
มีการกำหนดเพิ่มเติมว่าปริมาตรรวม หรืออีกชื่อหนึ่งสำหรับพื้นที่ปิดหรือลูกบาศก์ เกิดขึ้นจากพื้นผิวขอบเขตด้านนอกของฐานอาคาร ผนังภายนอก และหลังคาที่มีหลังคา พูดง่ายๆ ก็คือพื้นผิวหลังคา ขอบด้านนอกของผนังภายนอก และแผ่นพื้นก่อให้เกิดขอบเขตของปริมาตรที่อยู่ระหว่างการพิจารณา บัดนี้เกิดคำถามขึ้นอย่างถูกต้องว่ารายละเอียดนี้จะจัดการอย่างไร ในแต่ละกรณี บ้านจะมีรายละเอียดจำนวนมาก ซึ่งขึ้นอยู่กับการตีความของ DIN ซึ่งอาจส่งผลให้มีปริมาณเพิ่มขึ้นหรือไม่ก็ได้ เพื่อให้เกิดความชัดเจนในที่นี้ จึงได้มีการควบคุมอย่างชัดเจนว่าส่วนประกอบของอาคารใดบ้างที่ไม่รวมอยู่ในการคำนวณลูกบาศก์:
- ฐานรากที่ลึกและตื้น เช่น ฐานรากและแผ่นพื้น
- เพลาไฟ
- บันไดและทางลาดภายนอก หากไม่ได้เชื่อมต่อกับอาคารอย่างมีโครงสร้าง
- กันสาดทางเข้า
- ยื่นหลังคา
- ระบบป้องกันแสงแดดแบบคานยื่น
- ปล่องไฟ ท่อไอเสีย และท่อระบายอากาศที่ยื่นออกมาเหนือกาบหลังคา
- โดมแสงที่มีปริมาตรเหนือเมมเบรนหลังคาสูงสุดหนึ่งลูกบาศก์เมตร
- ปลูกไม้เลื้อย
- ที่นั่งหรือเฉลียงกลางแจ้งที่แข็งแกร่ง แม้ว่าจะยื่นออกมาจากพื้นดินก็ตาม
กรณีพิเศษ
ส่วนของอาคารที่ไม่ได้ปิดสนิทจะมีตำแหน่งที่ค่อนข้างพิเศษในการคำนวณปริมาตร ตัวอย่างนี้รวมถึงหลังคาบนส่วนรองรับที่ไม่มีผนังปิด โดยทั่วไปจะพบห้องใต้หลังคาหรือเชิงเทินระเบียง เช่น ส่วนของผนังแนวตั้งที่ไม่มี "ที่กำบัง" ด้านบนในรูปของหลังคาในที่นี้ DIN ระบุอย่างชัดเจนว่าสิ่งที่เรียกว่าส่วนประกอบสมมติสามารถและต้องใช้เพื่อกำหนดขอบเขตพื้นที่
นี่หมายความว่าอะไร?
หมายความง่ายๆ ว่าขอบด้านบนของห้องใต้หลังคาแสดงถึงขีดจำกัดด้านบนของปริมาตรที่เกิดขึ้นในลักษณะนี้ ในกรณีของหลังคา ผนังด้านนอกสมมติจะถูกกำหนดโดยส่วนรองรับ หรือ - หากยื่นออกไปโดยไม่มีส่วนรองรับ - โดยขอบของหลังคา
หมายเหตุ:
การกำหนดขอบเขตขอบหลังคาและหลังคาไม่ใช่เรื่องง่าย เนื่องจากขอบหลังคาบางส่วนมักจะถูกขยายให้ใหญ่ขึ้นจนกลายเป็นหลังคาระเบียง ที่นี่ปกติใช้ระยะได้ไม่เกิน 0.50 เมตร หากส่วนยื่นของหลังคามีขนาดใหญ่ขึ้นก็ถือเป็นหลังคาที่สร้างช่องว่าง สูงถึง 0.50 เมตร นี่คือขอบหลังคาที่ไม่ได้คำนึงถึง
การคำนวณโดยใช้ตัวอย่างทีละขั้นตอน

ตอนนี้เรามาดูการคำนวณปริมาตรโดยใช้ตัวอย่างที่เป็นรูปธรรมกันดีกว่า เป้าหมายในการกำหนดปริมาณของเรา เราจะพิจารณาบ้านเดี่ยวทั่วไปที่มีลักษณะดังต่อไปนี้:
- ยาว 10 เมตร
- กว้าง 8.5 เมตร
- ความสูงเชิงชาย (ความสูงจุดตัดของผนังภายนอกพร้อมกาบหลังคา=จากภูมิประเทศ 3, 50 เมตร
- สันเขา สูง 6.00 เมตร
- ชั้นใต้ดิน ขอบด้านบนของแผ่นพื้น 3.00 เมตร ใต้ดิน
- หลังคาทรงจั่ว
- หลังคายื่น 0, 30 เมตร
- ห้องโถงต่อเติม กว้าง 1.00 เมตร ลึก 1.50 เมตร สูงจากพื้นดิน 3.00 เมตร หลังคาเรียบ
- ส่วนต่อเติมหลังคาลานรองรับระยะห่างจากขอบบ้าน 3.00 เมตร และกว้าง 3.00 เมตร หลังคาเรียบ ความสูงจากพื้น 2.50 เมตร
ทีละขั้นตอน
1. การสลายตัวทางจิตเป็นปริมาตรบางส่วนที่จับต้องได้:
- ตัวบ้าน ขอบบนของพื้นถึงความสูงของชายคา
- ชายคาหลังคาสูงถึงสันหลังคา
- กระจกบังลม
- หลังคาระเบียง
2. การกำหนดสูตรทางคณิตศาสตร์สำหรับการคำนวณปริมาตรของโครงสร้างย่อย:
ก.ตัวบ้าน: ยาว x กว้าง x สูง
ข.หลังคา: ยาว x กว้าง x สูง x 0.5
ค.ตัวดักลม: ยาว x กว้าง x สูง
ง.หลังคาระเบียง: ยาว x กว้าง x สูง
3. การคำนวณปริมาณ:
ก.ตัวบ้าน: 10, 00ม. x 8, 50ม. x (3, 50ม.+3, 00ม.)=552, 50ม.3
ข.หลังคา: 10.00ม. x 8.50ม. x (6.00ม. - 3.50ม.) x 0.5=212.00ม.3
ค.กันลม: 1.50ม. x 1.00ม. x 3.00ม.=4.50ม.
ง.หลังคาระเบียง: 3.00ม. x 3.00ม. x 2.50ม.=22.50ม.
e.ซำ ถึง d.=791, 50m³
หมายเหตุในการคำนวณ
ตัวอย่างแสดงให้เห็นว่าการคำนวณลูกบาศก์นั้นง่ายมากด้วยวิธีการที่ถูกต้อง คำแนะนำและเคล็ดลับเหล่านี้จะช่วยให้คุณบรรลุเป้าหมายโดยไม่มีข้อผิดพลาด:
ผ่า

แจกแจงโครงสร้างที่จะคำนวณเป็นแต่ละวอลุ่มที่ง่ายต่อการคำนวณมากที่สุด ซึ่งหมายความว่าคุณสามารถใช้สูตรสำหรับทรงลูกบาศก์หรือทรงสามเหลี่ยมที่รู้จักตั้งแต่สมัยเรียนได้เกือบทุกครั้ง
ระยะห่างของหลังคา
ไม่ว่าหลังคาจะชันแค่ไหนและไม่ว่าจะสมมาตรหรือไม่สมมาตร หลังคาแหลมสามารถคำนวณได้เสมอโดยใช้สูตร ยาว x กว้าง x สูง x 0.5 แม้แต่หลังคาหน้าจั่วก็สามารถคำนวณได้ด้วยวิธีนี้หากคุณเข้าใจว่าเป็นหลังคาหน้าจั่วรูปแบบพิเศษที่มีพื้นผิวหลังคามีความเอียง 90 องศา
ขอบล่างสำหรับส่วนประกอบพิเศษ
ไม่ว่าจะเป็นห้องโถงหรือหลังคาระเบียง เมื่อใดก็ตามที่ไม่มีขอบด้านล่างของโครงสร้าง พื้นผิวภูมิประเทศก็สามารถมองเห็นได้ว่าเป็นขีดจำกัดล่างของปริมาตร ตัวอย่างเช่น หากห้องโถงตั้งอยู่บนพื้นที่ลาดเอียง ให้ใช้ความสูงของภูมิประเทศที่ประตูทางเข้าเป็นความสูงที่เกี่ยวข้อง

